Отсутственность – как основной постулат математики…

Некоторые считают, будто математика полезна для физики и техники.
                  Истинная же польза в том, что если бы вместо проблемы Ферма
                  математики занимались бы усовершенствованием автомобилей или самолетов,
                  то вреда было бы гораздо больше.
                                   Харди. Директор Математического института Макса Планка

   Cтолкнувшись с многочисленными загадками природы, современный ученый не может
   не испытывать чувства радости, если их удается «похоронить» под грузом математических
   символов, причем совершить погребение столь тщательно, что многие последующие
   поколения ученых не в состоянии обнаружить вход в гробницу.
                                   Морис Клайн, из книги «Математика. Поиск истины»:

Любому человеку ясно истинное предназначение науки, которое, конечно же, должно заключаться не столько в описании окружающего мира, сколько в формировании и развитии в ней прогностического потенциала. Человечество чтит великими тех людей, которые пусть немного, но смогли заглянуть в будущее. А отыщутся ли в нескончаемом перечне современных «отраслей знаний» научные дисциплины, могущие похвалиться такими достижениями?  Те ли это, что чтут себя точными науками и с помощью хитроумных и сложных экспериментов пытаются проникнуть даже вовнутрь элементарных частиц материи? Или это различного рода технологии, во главе с активно рекламируемой генной инженерией? А может «чистое знание» царицы точных наук - математики? Нет, нет и нет! Даже опыт существования современной цивилизации свидетельствует только об обратном. Более 40% всех Нобелевских премий присуждается за те работы, которые со временем оказываются ошибочными. Из продуктов питания сегодня в первую очередь покупаются только те, где есть упоминание об отсутствии ГМО. Место жительство люди стремятся выбрать, если, конечно, это им по силам, в экологически чистых районах, а атомную энергетику боятся как чёрт ладана. Так, что смысл слова наука постепенно приобретает отрицательный оттенок. Показательно, что математика, освящая все научные исследования (даже гуманитарные), дальновидно стремится обезопасить себя, «научно» обосновав свою прогностическую импотенцию теоремой Геделя…. Что же всё это значит? А то, что, пытаясь ответить на вопросы: «Почему?», «Кто виноват?» и «Куда идти?», - мы должны в своих исследованиях не только подняться до мировоззренческого уровня, но и вплотную приблизиться к сакральным знаниям. Конечно такой «замах» в намерениях может показаться самонадеянным, но и столь любимое нами безделье нас не украсит. Давайте попробуем хотя бы осветить некоторые проблемы.

                                    О РАЗНЫХ МЕРНОСТЯХ …
Из курса начальных классов любой школьник знает, что произведение двух чисел a и b есть ни что иное, как краткая запись сложения, то есть a b = а + а +…+ а (b слагаемых). Казалось бы, простое и очевидное правило. Однако последующая учёба в институте принуждает нас отказаться от наглядности этих представлений, и переводит наше мышление в абстрактное поле логической непротиворечивости. Так, например, в понятийном поле математического анализа произведениепочему-то становится неопределённостью, которую следует раскрывать по соответствующим теоремам о пределах. Хотя, следуя очевидным правилам арифметики, легко убедиться, что сумма любого количества нулей [1] в итоге так и останется нулём.

Институтские «знания», потесняющие наглядность, вносят серьёзную сумятицу в наши головы. Но это, как говорится, ещё только цветочки. Желающим «углубить» свои познания услужливо предлагают вкусить и ягодки. Даже «сакральным» смыслом произведения  готовы поделиться. Так из книги Гаухмана «Алгебра сигнатур» [2] можно узнать, что при «перемножении отсутственности с бесконечностью получается парадоксальная конечная единственность».

К сожалению, парадоксальность заключается как раз в том, что в фундаменте современной науки обосновались не наглядность, простота и очевидность, а эта самая абстрактная отсутственность с её «удивительными» свойствами. И в этом можно убедиться на многих примерах. Начнём хотя бы с мерности, так любимой писателями фантастами, путешествующими в n-мерных Вселенных.

О размерностях люди издавна имеют вполне здравые представления, и только с лёгкой руки Евклида геометры линией стали называть длину без ширины (почему-то обратили внимание не на её длину, которая несёт в себе информацию, а на неинформативную ширину). Человеку, воспитанному в наглядном восприятии окружающего мира, невозможно понять длины, не имеющей ширины, ни в чувственном, ни в умопостигаемом плане, так как, по здравому смыслу, с исчезновением толщины исчезнет и сама линия, причём не только в пространстве, но и на плоскости. Математикам проще: они, следуя принципу Поля Дирака «Заткнись и считай», легко избавляются от этого «комплекса неполноценности».  

Рассмотрим, как современные учёные переходят от одной топологической размерности пространства к другой[3]. Например, надо объяснить «четырёхмерное пространство». Популяризаторы для этой цели используют принцип аналогии, рассматривая, якобы понятный всем, двумерный мир как предельный переход от трёхмерного. Для наглядности представления берут батон колбасы и режут его на тоненькие–тоненькие «колясочки». Такие тоненькие, что их толщиной можно пренебречь. Эти «колясочки» и есть в представлении популяризаторов двумерный объект. А лауреаты Нобелевской премии по физике за 2010 год толщину графитового слоя опилок от карандашного грифеля, нанесённого на липкую поверхность скотча, уменьшали, многократно приклеивая к опилкам чистые ленты, и затем отрывая их. После определённого числа таких манипуляций слой графита утоняется до молекулярной толщины и, по мнению «нобелеатов» становится двумерным кристаллом, который, якобы приобретает свойство нового материала – графена.

Если же провести все действия в обратном порядке, и сложить друг с другом все «колясочки» (или снятые скотчем слои графита), то получится исходная трёхмерная структура (батон колбасы или куча опилок). Таким образом, якобы можно, исследуя свойства найденного «двумерного мира» и его отличия от трёхмерного, экстраполировать полученные знания на четырёхмерный, а от него на пятимерный, и так до бесконечности….

Но в том-то и дело, что эта популистская аналогия есть не что иное, как обыкновенный софизм, или умышленный обман, прикрытый авторитетом Евклида. Остановимся на этом немного подробнее.  

Получение двумерной топологии в рассмотренных примерах тесно связано с бесконечно малыми величинами (б/м), предельный переход которых к нулю обосновывается  аппаратом математического анализа. Однако обратный переход от нуля к б/м логически непротиворечивого обоснования не имеет. А без него сложение нулей друг с другом даст вполне ожидаемый и, главное, очевидный результат, однозначно запрещающий переход от «двумерии» к «трехмерии».

Интересно, что в физике соотношением Гейзенберга запрещается и прямой переход от б/м к нулю, так как б/м не может, в соответствии с требованиями процедур перехода, быть меньше любого наперёд заданного и сколь угодно малого числа.

Законы физики устанавливают и другой запрет на существование двумерных фантазий. Я говорю о физических взаимодействиях, описываемых векторными произведениями, которые работают только в пространственных координатах. Так что рассуждать об известном правиле «буравчика» или о кориолисовой силе в «двумерии» не только бессмысленно, но и безграмотно[4].

Таким образом, приведённая аналогия для объяснения перехода из трёхмерного измерения в четырехмерное и выше - несостоятельна. Но принцип Дирака толкает и толкает математиков в область манящих мнимостей. Рассмотрим одну из них.            

                                          ФРАКТАЛЫ
Напомним, что фрактальное множество - самоподобная структура - один из «горячих» объектов современной «нелинейной» науки[5]. Подобные объекты были известны довольно давно, но настоящий интерес к ним появился после активной популяризаторской деятельности Бенуа Мандельброта, работающего в корпорации IBM. Именно он ввел название «фрактал», связанное с дробной размерностью подобного необычного объекта, и указал на чрезвычайно широкое распространение этих объектов в нашем мире.

Прежде, чем разобрать суть этой геометрической модели границ взаимодействующих объектов, обратимся к этимологии этого слова (недаром же говорят: «Как назовёшь, так и будет жить[6]»). Фрактал от латинского «фрактус» означает дробный, нецелый. Но судить о целом по его части, значит уподобиться слепцам, ощупывающим разные места слона (хвост, хобот, ногу и т.д.) и делающим на основании своих впечатлений соответствующие умозаключения о его внешнем виде. Можно ли границу между объектами рассматривать в отрыве от самих объектов? Конечно, нельзя! Поскольку часть без целого не живёт, а всего лишь безжизненно существует. Это широко используемая в природе обманка против хищников: отброшенный, но шевелящийся хвост ящерицы или чернильный образ стремительно уплывающего в противоположную сторону кальмара. Именно поэтому дальше можно не проводить глубоких исследований об онтологической полезности «изобретения» Мандельброта. Тем не менее, убедимся, что поговорочная традиция нас и в этом случае не обманула.

Начнем с самоподобия. Самоподобие есть свойство нашего трёхмерного мира, однако математики, добавив в рассмотрение бесконечно малые и бесконечно большие величины,  довели это свойство до абсурдной, зато «прекрасной картины» бесконечной Вселенной. Суть самоподобия фрактальщики поясняют на следующем примере. Представьте себе, что перед вами снимок «настоящей» геометрической прямой, «длины без ширины», как определял линию Евклид, и вы забавляетесь с приятелем, пытаясь угадать, предъявляет ли он вам исходный снимок (оригинал) или увеличенный в нужное число раз снимок любого фрагмента прямой. Как бы ни старались, вам ни за что не удастся отличить оригинал от увеличенной копии фрагмента: прямая во всех своих частях устроена одинаково, подобна самой себе[7].
Мы видим здесь яркое проявление ряда «новых» свойств отсутственности. Оказывается, отсутственность можно наблюдать (!?), но увеличить её изображение нельзя, точнее можно, но только в направлении другой мерности (длины). Именно эта не существующая в природе анизотропия и легла в основу всех фрактальных «научных» моделей.
А вот другая аналогия самоподобия, в которой отсутственность трансформируется в мнимость. Это картинка видеообратной связи, простейшим примером которой служит изображение, получаемое в зеркале, отображающем другое зеркало, стоящее напротив. Наблюдатель, помещенный между двумя плоскими зеркалами, видит некоторую бесконечную картинку, полученную в результате многократных отражений. Зеркала отображают бесконечность мнимых изображений, чего вне этих зеркал нет.
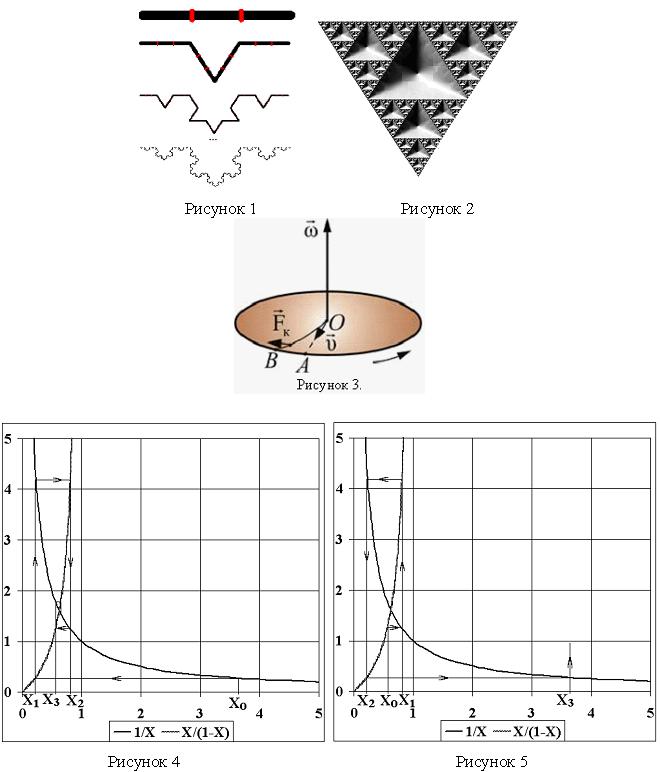
Интригующим свойством фрактала является его дробная размерность. «Как же может в нашем трехмерном пространстве появиться дробная размерность?», – спросите вы. С точки зрения фрактальной геометрии легко: по договоренности! Вот, например как строится звезда Коха (рисунок 1).
В начале берётся отрезок, делится на три равные части и средняя часть заменяется на два отрезка, равных изъятому. Получается ломаная из четырёх равных отрезков. На втором шаге действия повторяются с каждым из четырёх отрезков, и получается ломаная из 16 отрезков.

Построения повторяются n раз и, в конце концов, получается ломаная, состоящая из бесконечного числа отрезков. Это и есть звезда Коха. Она состоит из N = 4n отрезков длины r = 1/3n. Значит, длина ломаной линии стремится к бесконечности L =(4/3)n. Отношение D = ln4/ln3 = 1,2619 не зависит от номера «поколения» и является характеристикой данной линии. Вычисливший её немецкий математик Хаусдорф назвал полученную дробь размерностью.
На этом примере мы можем подивиться и другими «открытиями» сопутствующими отсутственности, а именно: звезду Коха можно замкнуть, и тогда бесконечная длина обоймёт конечную площадь. Этот факт явно должен льстить имперскому самолюбию Великобритании. Как же! Ведь Мандельброт в своей книге таким способом доказал, что протяженность её границ бесконечна!
А вот ещё одна любопытная фрактальная фигура - салфетка Серпинского (рисунок 2), которая, имея бесконечную длину каркаса, занимает нулевую площадь.

При этом фрактальщиков не смущает, что сопоставляются разные размерности. Евклид не смог, точнее знал, что нельзя сравнивать площадь с объёмом или с линией, но у изобретателей фракталов – всё получается легко и логически непротиворечиво. Мы уж не говорим, что на первом шаге построения звезды Коха, одномерная прямая была преобразована в двумерную ломаную линию, которой потом зачем-то присвоили дробную размерность. «Какие основания?». Договоренность …
Кто-то сказал, что фрактал - это, межвидовой потомок, своего рода ублюдок. Сказано точно, посмотрите:
Например, фрактал, как множество точек, не является ломаной, состоящей, по определению, из конечного числа отрезков. Однако фрактальное множество обладает свойствами ломаной: к нему невозможно провести касательную, и взять производную.
Или ещё: фракталы - это язык геометрии, которой присуща очевидность. Однако главное свойство фракталов - бесформенность, их элементы недоступны непосредственному наблюдению. И в этом отношении они принципиально отличаются от привычных объектов евклидовой геометрии. Фракталы выражаются не в первичных геометрических формах, которым свойственна законченность, а в алгоритмах, наборах математических процедур, неограниченных ни во времени, ни в пространстве, и которые трансформируются–то в геометрические фигуры только с помощью компьютера.
Но главное, несмотря на повсеместно наблюдаемое распространение объектов с самоподобной структурой, природа не экстраполирует самоподобие в сторону бесконечно малых и бесконечно больших, что говорит о нелинейности коэффициента подобия и насыщении со стороны как минимума (постоянной Планка), так и со стороны максимума (конечность энергии[8]).
Здесь прямо-таки напрашивается аналогия с голограммой. Известно, что в каждом элементе голограммы содержится информация не только об интенсивности излучения всех точек объекта, но и о расстоянии до каждой точки. Поэтому даже от небольшого осколка голограммы, подсвеченного соответствующим лазером, можно получить действительное изображение объекта. Осколок может быть очень маленьким. Однако никому не придёт в голову, на этом основании, сделать вывод, что размеры осколка можно устремлять к нулю. Любому ясно, что голограмма получена с помощью реальных физических объектов, обладающих конкретными свойствами, а именно длиной волны лазера и размерами чувствительных гранул фотопластинки. Естественно поэтому ожидать ухудшения чёткости изображения при уменьшении размеров осколка, что и наблюдается на практике.
Фрактальность природных образований также наблюдается в ограниченных пределах, но математика, подчиняясь требованиям «чистой науки», и пользуясь определением Евклида, устремилась к нулю. Результат: мы имеем ещё одну теорию отсутственности, то есть того, что в природе нет, да и быть не может!      
Большие надежды, возлагаемые на фракталы как на средство описания хаоса, тоже не оправдались, да и описывает они (по словам того же Мандельброта[9]) только самоподобную часть хаоса. А вопрос: «Какая это часть и  могут ли фракталы быть описанием хаоса в отсутствии самого определения хаоса?», - повис в воздухе.
В общей теории систем термин “фрактал” не состоялся[10]. И это, пожалуй, единственное, что наука сделала правильно на поприще увлечения фракталами. Мне кажется, эволюция была бы скучной и холодной, убогой и бессмысленной, если бы заключалась только во фрактальности - бесконечном повторе исходных структур. От этого веет безысходностью рассказов Екклесиаста, известного библейского персонажа: «…. всё возвращается на круги свои, … всё суета сует». Но ум и чувства протестуют против такого «дробомерного» понимания эволюции.
Незаменимыми фракталы оказались лишь в машинной графике и киноиндустрии, при генерации искусственных облаков, гор, поверхности моря. С их помощью был найден способ легкого представления сложных неевклидовых (а точнее, мнимых) объектов, образы которых весьма похожи (но и только!) на природные….
Безобразный горбун Квазимодо из «Собора Парижской Богоматери», безнадёжно влюблённый в красавицу Эсмеральду, тайком наблюдая за её игрой с любимой козочкой, сокрушался, что не может быть на месте ласкаемого животного, которое, если приглядеться, было безмерно страшнее его. А беда-то вся заключалась в том, что он, при всём своём уродстве, всё-таки, оставался похожим на человека.  

                                     СОН НЬЮТОНА
По устоявшему сегодня мнению «Начала Натуральной Философии» Ньютона составляют незыблемое основание механики, теоретической астрономии и физики. А Лагранж в своё время даже назвал это сочинение «величайшим из произведений человеческого ума». Но почему же тогда английский поэт Блейк (почти их современник) выразил своё, по-видимому, отрицательное отношение к «Началам…» такими словами: «Да спасет нас бог от одностороннего видения и Ньютонова сна»?

О каком сне поэт говорит? Сон в обыденном понимании - такое состояние, которое смертью вроде бы не назовёшь, но и жизнью нельзя считать, особенно если сон летаргический. Что Блейк имел в виду?

Вот уже многие десятилетия авангард науки безуспешно бьётся над созданием теории ВСЕГО. Электромагнетизм, слабые и сильные взаимодействия – все послушно объединились в Стандартную модель, а ньютоновская гравитация – как киплинговская кошка - сама по себе. Каждый вид взаимодействия имеет полярные составляющие (плюс - минус, север – юг), а у гравитации Ньютона опять свое собственное мнение. И наука никак не подыщет ей полярную пару. В чём дело?

В статике магнитное поле и электрическое поле друг с другом не взаимодействуют. То есть маленький магнитик не шелохнётся в электростатическом поле, а электрон не сдвинется в магнитном. Но если электрону, находящемуся в магнитном поле, сообщить постоянную скорость (для определенности скажем в направлении, перпендикулярном силовым магнитным линиям), то он дополнительно приобретёт ускорение,  причём не по магнитным линиям от северного полюса к южному, а перпендикулярно им, так, что его результирующее движение будет спиральным. Этот процесс описывается с помощью векторного произведения, известного в физике как правило левой руки.

В механике Ньютона такого вида взаимодействия отсутствуют, но если не по Ньютону, а в природе, то они есть! Например, на тело, движущееся относительно вращающейся системы отсчета, действует сила Кориолиса Fк . Эта сила направлена перпендикулярно плоскости, проходящей через вектора угловой скорости w и скорости движения тела v так, что тройка векторов Fк, w, v образует векторное произведение: Fк=2mvxw (рисунок 3). При этом, если диск не вращается, то шарик, запущенный в направлении от О к А со скоростью v, будет катиться вдоль ОА. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой ОВ, причем его скорость относительно диска быстро изменяет свое направление.  

В «величайшем из произведений человеческого ума» сила Кориолиса не является «настоящей». Она, так же как и Деламберовы и Эйлеровы силы, при рассмотрении динамики объектов в неравномерно движущихся системах отсчёта, вводится искусственно, чтобы  придать уравнениям движения в таких системах формально такой же вид, как и в инерциальных системах отсчета (как говорят в народе, телегу ставят впереди лошади!). По Ньютону получается, что траектория движения шарика ОВ есть, но сила, которая заставляет его так двигаться, – отсутствует. Турбину на гидроэлектростанции вода вращает силой своего течения (падения), но в известном природном явлении (законе Бера) соответствующие берега рек, текущих в меридиональном направлении, вода размывает уже не силой своего течения, а своим свойством – инерцией....

Всё потому, что «Начала …» рассматривают только инерциальные системы отсчета, в которых указанные силы не существуют. Но природа-то как раз состоит из неинерциальных систем, а инерциальные появляются только в виде предельного перехода, когда влияние окружающей среды устремляют к нулю.

Вы чувствуете опять присутствие нашей старой знакомой - отсутственности? Опять нас толкают в эту пресловутую «нирвану» - отсутствие всякого присутствия! Это она видна из первого закона Ньютона, утверждающего неразличимость состояние покоя или равномерного и прямолинейного движения в механических системах. Это на ней основан принцип относительности Пуанкаре, который  распространяет отсутственность на все физические явления. И, конечно же, это она венчает «вершину» наших сегодняшних знаний – теорию относительности. Инерциальных систем в природе нет, однако теория их описывающая имеется.                 Наш Поэт считал по-другому:
                           Движенья нет, сказал мудрец брадатый.
                           Другой смолчал и стал пред ним ходить.
                           Сильнее бы не мог он возразить;
                           Хвалили все ответ замысловатый….
Некоторые отметят: «Да разве это возражение? Ведь всё в мире относительно!». Именно возражение, да ещё какое, не в бровь, а в глаз! Диоген-то показал Зенону абсолютное движение. Он «стал пред ним ходить». Что значит «пред ним»? Значит туда-сюда, то есть совершать колебательное движение! А вращательные и колебательные движения  продолжали и продолжают сохранять абсолютный характер, несмотря на появление законов Ньютона и теории относительности.

Обратите внимание, что основным кинематическим следствием природных взаимодействий является циклическое (вихревое) или колебательное движение. И это важно, поскольку наблюдаемое явление есть не что иное, как дыхание жизни. А Ньютон, исключив из своего рассмотрения такие взаимодействия, увлёк нас в сторону летаргического сна.

Выходит прав был Блейк и в отношении односторонности, и в отношении Ньютонова сна!


                      СИСТЕМЫ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
Вопрос: «Что такое система уравнений?» - никого, наверное, не затруднит. Более того, многие смогут вспомнить и некоторые методы решения систем алгебраических уравнений. Например, метод подстановки или замену одного уравнения суммой нескольких других уравнений и т.д. Но уверенно рассказать об итерационном методе решения простой системы уравнений, наверное, сможет далеко не каждый, хотя слово «итерация» наверняка слышали все. И уж тем более пояснить причины (не условия, а причины!) расходимости или нерасходимости итераций при решении уравнений затруднится даже математик высокой квалификации.

Запишем, например уравнение деления отрезка в среднем и крайнем отношениях:
1/x=x/(1-x),                                                                 (1)
где единицей обозначен целый отрезок, х - больший его отрезок, а (1-х) – меньший.

Сначала решим это уравнение алгебраическим методом. После преобразования получим квадратное уравнение х2+х-1=0, решение которого даёт два корня: x'=-1,618 и x"=0,618.

С точки зрения поставленной задачи (а имеется в виду деление отрезка в среднем и крайнем отношениях) алгебраическое решение поступило по принципу «Мы ему про Фому, а он нам про Ерёму». Оно, во-первых, добавило несуществующий в природе отрицательный корень, а во-вторых, исключило порядок действия в рассматриваемом процессе (а это означает, ни много - ни мало, нарушение причинно-следственных связей!). И если с первым алгебраист как-то согласится, то последнее замечание для него будет выглядеть бессмысленным и даже надуманным, поскольку в алгебре равенство всегда обратимо и, более того, все алгебраические правила преобразований строятся как раз на этом свойстве равенства: перенос членов уравнения по другую сторону равенства, умножение и деление левой и правой части уравнения на одно и то же число и т.д.

Не будем спорить, давайте решим уравнение методом простой итерации. На рисунке 4 показана последовательность решения итерациями уравнения 1, когда началом процесса итерирования является произвольно взятая точка (с абсциссой хо) на кривой 1/х. Видно, что уже после нескольких итераций мы получаем решение, то есть абсциссу, близкую к точке пересечения двух кривых. И наоборот, начав итерации с точки хо на кривой х/(1-х), мы уже на третьей итерации (по рисунку 5) удаляемся от решения в бесконечность [11].

Чтобы понять, что сие означает, вернёмся к постановке задачи. Мы хотели разделить отрезок в определённой пропорции. То есть изначально мы имели целый отрезок и знали его длину, а затем приступили к его делению. Такая последовательность действий не представляется бессмысленной и отражена на рисунке 4.

Рисунок 5 иллюстрирует последовательность, когда первое действие совершается в отсутствии самого отрезка и знаний о нём. Наши действия начинаются с абсциссы Хо и уже на третьей ступени уходят от точки пересечения в бесконечность. Как будто итерация подсказывает нам, что знания отношения произвольно взятых отрезков и их суммы не позволят решить поставленную задачу в отсутствии информации об исходном отрезке. Очевидно, что в таком порядке решать задачу невозможно.

Иначе говоря, алгебраические методы решения систем линейных уравнений исключают (то есть превращают в отсутственность) время из описываемых явлений, относясь безразлично к направлению равенства. Как результат, одно из решений получается бессмысленным, и мы вынуждены проводить их проверку, но не подстановкой в исходное уравнение (оба решения окажутся с точки зрения алгебры подходящими), а из практической целесообразности, отбрасывая решение с отрицательной длиной. Напротив, итерационный метод оставляет время в исследуемых процессах, рассматривая их с точки зрения порядка действия природных связей. Поэтому итерации оказываются чувствительными к последовательности предъявления исходных данных. В частности для нашего случая решение получается, только если «целое прежде своих частей».

Это очень важный момент. В Евангелии сказано: «Ищите, и обрящете…»[12]. Но делать – не значит сделать. Искать, не зная, что, как и где - значит обречь себя на неудачу. Именно поэтому Солоухин в своей книге «Третья охота» писал: «Известно, для того чтобы увидеть в лесу нужный гриб, птицу, притаившуюся в ветвях, птичье гнездо, орех на ветке, одним словом, все, что редко попадается и так или иначе прячется от глаз, надо держать в воображении то, что ищешь». И именно за отсутствие таких способностей и умение лишь усидчиво заседать, Ленин прозвал Молотова «каменной ж…пой».

Таким образом, все найденные нами следствия с отсутственностью являются не чем иным, как «чистой наукой», описывающей не реальный, а мнимый мир или, если говорить по-фрактальски, - виртуальную реальность (недаром фракталы приняли в свои объятия только компьютерщики). И это, к сожалению – знак времени! Даже современных писателей – новых инженеров человеческих душ - больше интересуют внешние эффекты, мрачные фантазии или фантасмагории, пародирующие действительность, но не сама жизнь.

Примечания

[1] По определению 0 – число, обладающее тем свойством, что любое число при сложении с ним не меняется.
[2]Михаэль Гаухман Алгебра сигнатур  (оранжевая Алсигна) “ИМЕНА”  Под редакцией и духовным руководством раввина Гавриэля Давидова. М.: Эдиториал УРСС, 2007.
[3] Напомним, что в математике традиционно пользуются понятием топологической размерности i, под которой понимают число измерений, необходимых для однозначного задания положения точки на геометрическом объекте. Обычно пользуемся приемами, которыми нас снабдила евклидова геометрия: точка имеет нулевую размерность, любая линия имеет одно измерение, плоскость - два измерения, куб - три измерения.
[4] Тем не менее, физики-теоретики, а вслед за ними и практики уже давно применяет законы электромагнитного взаимодействия для двумерных «электронных газов» и это их не смущает. Сюда относятся и классические работы из квантовой механики:  - квантовый эффект Холла (Клаус фон Клитцинг – нобелевский лауреат 1985 года); - дробный эффект Холла, где обнаружили не только двумерный газ, но и дробный заряд (Нобелевская премия 1998 года) и т.д.
[5]Андрианов И. Кто открыл фракталы. Знание-сила, 1997, №11.
[6] Мандельброт использует римскую пословицу: «Nomenestnumen» – «назвать - значит узнать» [Мандельброт Б. Фрактальная геометрия природы. М.: Институт компьютерных исследований. 2002г.].
[7] Данилов Ю.А. Фрактальность. Знание - сила, 1993г. №5.
[8] Кстати, если энергия была бы бесконечной, то бессмысленность существования закона сохранения энергии была бы очевидной.
[9] «Моя атака в новой области, - пишет Мандельброт в своёй книге «Фрактальная геометрия природы», - имела целью разделить на части понятие хаоса. Одна часть при этом так и осталась нетронутой, поскольку мы не знаем, как ее исследовать. Вторая же, хотя и менее общего вида, но весьма внушительная, заслуживает быть выделенной. Ее следовало бы изучить, хотя бы в силу многочисленности примеров самоподобия в природе, а еще потому, что именно из-за самоподобия она вполне поддается изучению».
[10] Материалы пятого Всероссийского постоянно действующего научного семинара "Самоорганизация устойчивых целостностей в природе и обществе". Н.Р. СухомлиновФракталы и циклы в эволюции живых систем http://pozdnyakov.tut.su/Seminar/a0101/a011901.htm.
[11] Впервые на это обратил внимание Быстров М.В.в своей книге «Вера и научное знание: Конец противостояния. (Метафизика духа)». Санкт-Петербург 2005
[12]Евангелие от Матфея (гл. 7, ст. 7—8 ) – на церковно-славянском.